如何实现一个高效的关键词过滤功能?—— DFA算法
一、前言
有一个关键词库,此时需要检索一段文本中是否出现词库中的关键词,该如何实现?
小白回答:将所有的关键词放入一个set集合,然后遍历集合一个个匹配那段文本,存在的关键词放入另一个集合。实现代码如下:
public class Test131 {
public static void main(String[] args) {
Set<String> wordSet = new HashSet<String>();
wordSet.add("产品经理");
wordSet.add("产品总监");
wordSet.add("程序员");
String content= "产品经理工作内容包含需求收集,需求分析,需求落地,项目跟踪,项目上线,数据跟踪以及对业务人员进行培训,协助运营、销售、客服等开展工作。";
Set<String> haveWordSet = new HashSet<String>();
for (String word : wordSet) {
if (content.contains(word)) {
haveWordSet.add(word);
}
}
System.out.println(haveWordSet);
}
}
// [产品经理]
思路很简单,也很容易理解,但是当关键词有几千、几万个时,性能会急剧下降。分析一下时间复杂度,遍历关键词是O(n),从文字段落检索的时间复杂度也是O(n),合起来就是O(n^2)。
有没有其他更优的解决方案呢?有!就是DFA算法!
二、何为DFA算法
DFA即Deterministic Finite Automaton,翻译过来就是确定性有限自动机。简单原理就是:在一个有限的集合,其中的元素都有两种状态,结束和继续(可以用0代表继续,1代表结束),可以从一个元素检索到下一个元素,直到元素的状态为结束为止。
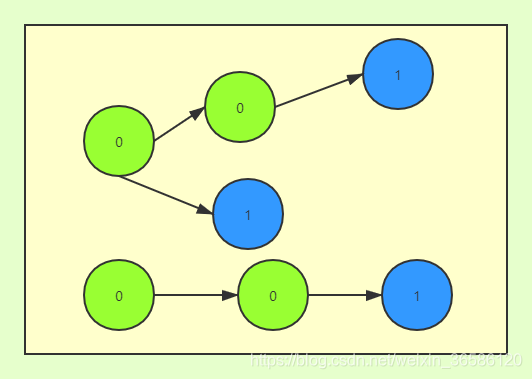
三、DFA算法优化关键词过滤
套用DFA算法的原理,例如有一些关键词:产品经理、产品总监、程序员,构建DFA算法容器如下:
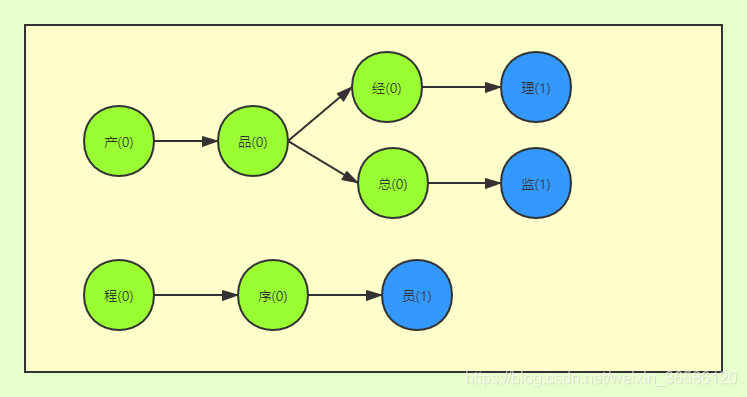
看着像一棵棵树,现在判断一个词是否在词库中,比如测试员,检索是否有”测“字开头的“树”,很快就能判断没有测试员这个词,比如检索“产品经理”,则可以找到”产“字开头的“树”,直接排除了“程序员”那棵“树”,这就大大缩小了范围。
算一下时间复杂度,从词库中匹配关键词,时间复杂度是O(1),遍历文字段落依然和文字的个数有关,时间复杂度最差(如果文本没有一个关键词)为O(n),合起来就是小于等于O(n)。使用DFA实现关键词过滤的优化点在于:检索的时间复杂度不会因为关键词数量的增加而受影响,只与被检索的文字长度有关。
四、java代码实现
分析数据结构,每一个字符都要存一个状态,可以用map实现,如果状态未结束还要存下一个字符的指针,也可以用map实现,这样就是map套map。如下:一个大map里有两个key,程和产,value值又是map套map。
{程={isEnd=0,
序={isEnd=0,
员={isEnd=1}
}
},
产={isEnd=0,
品={isEnd=0,
总={isEnd=0,
监={isEnd=1}
},
经={isEnd=0,
理={isEnd=1}
}
}
}
}
完整代码示例:
public class Test131 {
public static void main(String[] args) {
String content= "产品经理工作内容包含需求收集,需求分析,需求落地,项目跟踪,项目上线,数据跟踪以及对业务人员进行培训,协助运营、销售、客服等开展工作。";
Set<String> wordSet = new HashSet<String>();
wordSet.add("产品经理");
wordSet.add("产品总监");
wordSet.add("程序员");
init(wordSet);
System.out.println("wordMap=" + m_kwWordMap);
Set<String> haveWords = getWord(content, MIN_MATCH_TYPE);
System.out.println("haveWords=" + haveWords);
}
/**
* 初始化DFA关键词容器
* @param words
*/
@SuppressWarnings({ "rawtypes", "unchecked" })
public static void init(Set<String> words) {
// 预先 设置初始容量,以免扩容影响性能。
Map wordMap = new HashMap(words.size());
for (String word : words) {
Map nowMap = wordMap;
for (int i = 0; i < word.length(); i++) {
// 转换成char型
char keyChar = word.charAt(i);
// 判断是否已经有一个map树,只有在一个词的首字符有用
Object tempMap = nowMap.get(keyChar);
if (tempMap != null) {
// 存在,则共享一个map树根
nowMap = (Map) tempMap;
}
// 不存在则构建一个map树,
else {
// 设置状态位
Map<String, String> newMap = new HashMap<String, String>();
// 判断是设置 0还是1
newMap.put("isEnd", i == word.length() - 1 ? "1" : "0");
// 给keyChar该字符设置状态位
nowMap.put(keyChar, newMap);
// 将状态位map赋值给nowMap,表示下一个字符的指针和状态位在同一个map里。
nowMap = newMap;
}
}
}
// 上面始终修改的是nowMap,最后形成的是wordMap,原因是,预先wordMap赋值给了nowMap,
// 使得wordMap和nowMap中的map地址值共享,更新了nowMap中的map就是更新了wordMap。
m_kwWordMap = wordMap;
}
/**
* 检索关键词
* @param txt 被检索的文本
* @param beginIndex 被检索文本的开始位置
* @param matchType 匹配类型
* @return 返回检索到的关键词长度,用于从文本中截取
*/
public static int checkWord(String txt, int beginIndex, int matchType) {
// 匹配标识数默认为0
Map nowMap = m_kwWordMap;
int matchFlag = 0;
int matchMaxFlag = 0;
for (int i = beginIndex; i < txt.length(); i++) {
char word = txt.charAt(i);
// 获取指定key
nowMap = (Map) nowMap.get(word);
// 存在,则判断是否为最后一个
if (nowMap != null) {
// 找到相应key,匹配标识+1
matchFlag++;
// 如果为最后一个匹配规则,结束循环,返回匹配标识数
if ("1".equals(nowMap.get("isEnd"))) {
// 将matchFlag赋值给matchMaxFlag,为的是,
// 后面要是继续按最大匹配原则匹配时,匹配不到则按最小匹配原则的结果为准。
matchMaxFlag = matchFlag;
// 最小规则,直接返回,最大规则还需继续查找
if (MIN_MATCH_TYPE == matchType) {
break;
}
}
}
// 不存在,直接返回
else {
break;
}
}
return matchMaxFlag;
}
/**
* 从文本中检索出关键词
* @param txt 被检索的文本
* @param matchType 匹配类型
* @return
*/
public static Set<String> getWord(String txt, int matchType) {
Set<String> set = new HashSet<String>();
for (int i = 0; i < txt.length(); i++) {
// 判断是否包含关键词,length > 0 有,且是关键词长度
int length = checkWord(txt, i, matchType);
// 存在,加入set中
if (length > 0) {
// 从原文中截取 并放入set
set.add(txt.substring(i, i + length));
// 减1的原因,因为for会自增
i = i + length - 1;
}
}
return set;
}
private static Map m_kwWordMap = null;
// 最小匹配原则,如果关键词中有中国和中国人,文本内容为“我是中国人”,最小匹配原则匹配出中国
public static final int MIN_MATCH_TYPE = 1;
// 最大匹配原则,如果关键词中有中国和中国人,文本内容为“我是中国人”,最大匹配原则匹配出中国人
public static final int MAX_MATCH_TYPE = 2;
}
// wordMap={程={isEnd=0, 序={员={isEnd=1}, isEnd=0}}, 产={品={总={监={isEnd=1}, isEnd=0}, isEnd=0, 经={理={isEnd=1}, isEnd=0}}, isEnd=0}}
// haveWords=[产品经理]
五、总结
- DFA算法利用map套map的原理,极大程度上优化了检索性能,时间复杂度为小于等于O(n),n是被检索文本的长度。
- DFA实现的关键词过滤,性能不再受限于关键词的数量,只与被检索的文本长度有关。
- DFA关键词过滤,是精准过滤,无法实现模糊过滤,如
我是*人,*匹配单个字符,%匹配多个字符。
参考:https://www.cnblogs.com/twoheads/p/11349541.html 需要注意该文章中checkWord函数最大匹配原则时是有bug的,本人的示例已加matchMaxFlag更正。
